How to build a 2-Way ANOVA Table
This guide is to help you nail your exams in statistics, so let’s dive right in.
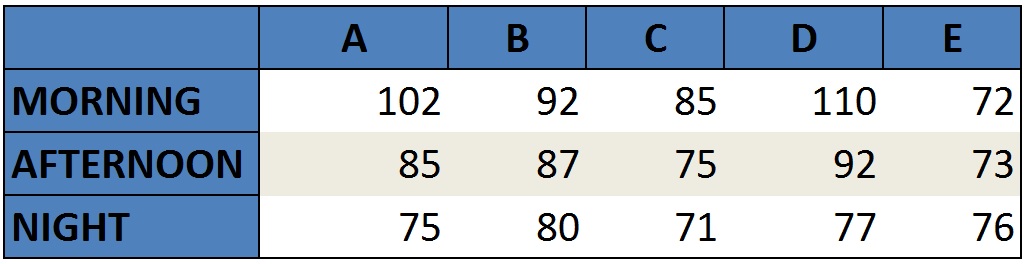
You will be given a table like the following picture. Let’s say each column represents 5 Stores from A-E and Each row represents Morning, Afternoon, and Night. The values refer to the average of people in each store during each period.
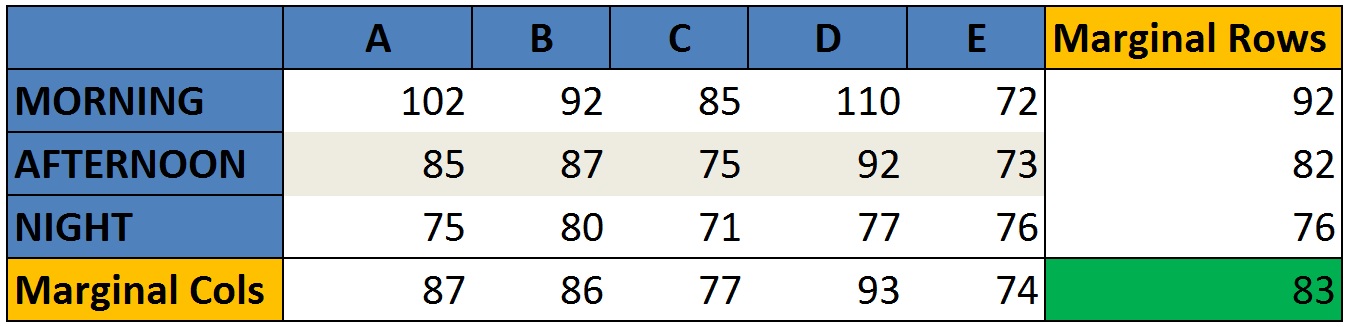
Step1: Add the Marginals and find the Averages
For each column fdo the average and the same for each row.
The green squarw with the value 83 is the averages. It doesn’t matter if you do (92+82+76)/3 or (87+86+77+93+74)/5. Both will lead to this same value.
Step2: Find Factor A and Factor B and TSS
We now have the Total Avg = 83.47
Factor A
Factor A(rows) = number of columns * the squared difference in the Marginal Rows(Top to Bottom)
5 * [(92.2-83.47)^2+(82.4-83.47)^2+(75.8-83.47)^2] = 680.93
Factor B
FactorB(Columns) = number of rows * the squared difference in the Marginal columns(Left to Right))
3 * [(87.33-83.47)^2+(86.33-83.47)^2+(77-83.47)^2+(93-83.47)^2+(73.67-83.47)^2] = 755.4
TSS
TSS is found bu doing the following:
find the sum of the square of each entry 102^2+… all the way to the last one+76^2 and subtract by the total number of entries n = 15 * TotalAvg = 83.47^2
This will give you a total of 1,859.7
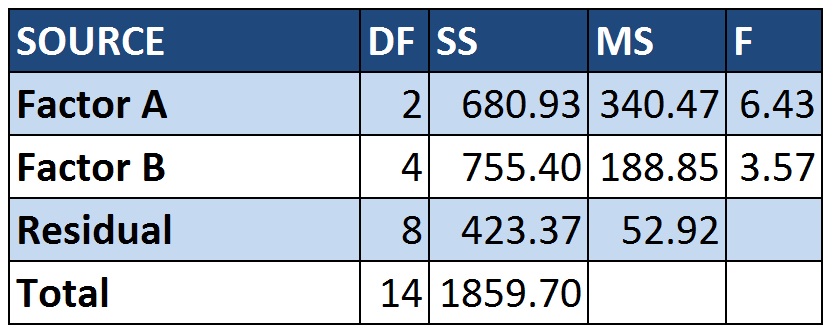
To build your 2-way anova table, you need to memorize: the headers: <Source>, DF(Degrees of Freedom), SS(Sum of Squares), MS(Mean Square), F-Test
Then for the rows you enter Factor A(always rows),Factor B(always columns), Residual or Error(same thing) and Total.
Finding DF’s (Degrees of Freedom)
The next step is to enter the DF.
Factor A: We have 3 rows, so the DF are 3-1 = 2
Factor B: We have 5 columns, so the DF are 5-1=4
Residual(Error): Multiply Factor A x Factor B = 8
Total: Sum Factor A + Factor B + Error = 2+4+8=14
Moving on, for the SS, we calculated SS for FactorA = 680.93, for Factor B = 755.40 and we also have the TSS which is 1,859.70, so to find the Residual we do the difference between the total and the rest which gives us the residual of 423.37
For the MS you just divide the SS by the DF. So for Factor A we have 680.93/2 = 340.47, for Factor B we have 755.40/4 = 188.85 and for the Residual we have 423.37 / 8 = 52.92
Finally to find F, you divide 340.47/52.92 = 6.43 for Factor A and for Factor B you do 188.85/52.92 = 3.57
Step3: Do the Test
They will ask something like this: “Use the analysis of variance to test whether there is any difference in the average number of people throughout the day(Factor A)”
They will usually tell you to use a specific significance level. Let’s say they tell you it is 5%.
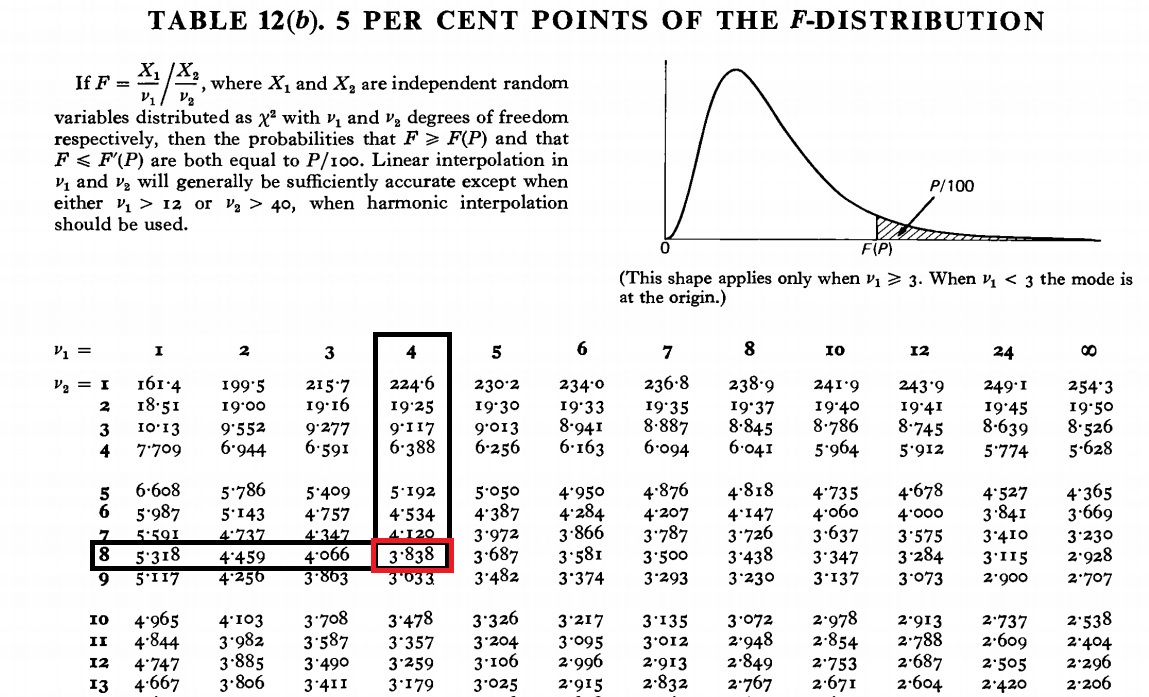
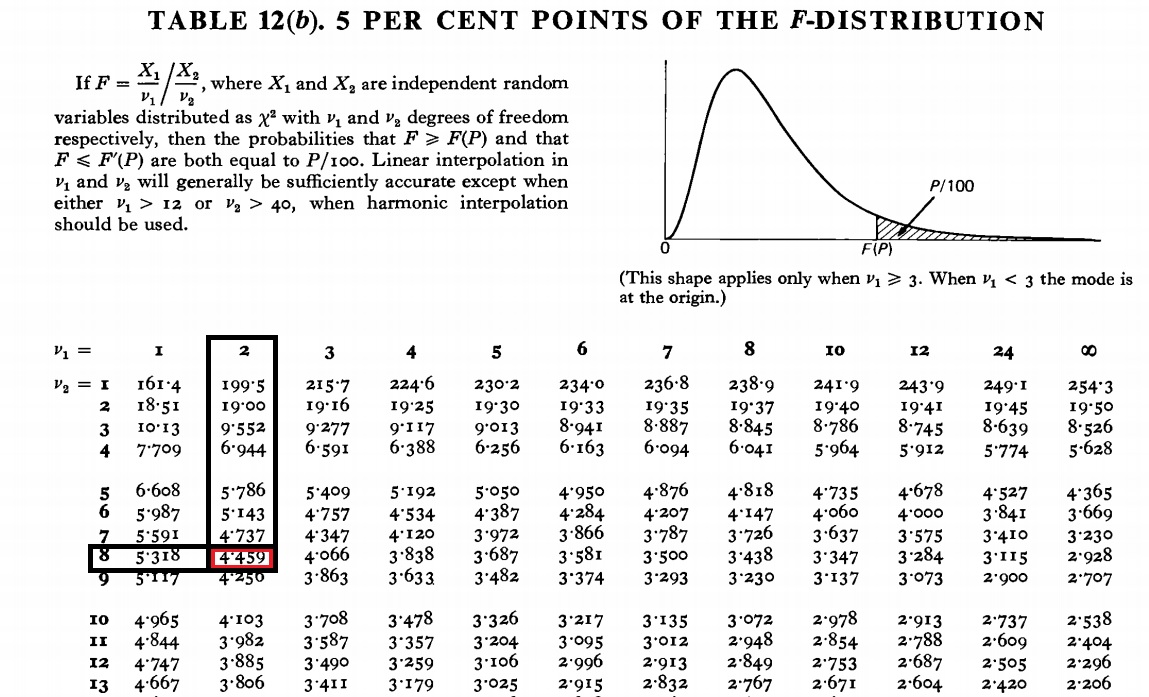
So what you do is use a Statistical F-Distribution Table at 5%(note that there are F-Tables for 10%, 2.5%, so make sure you are using the right one)
And you now have the needed values to find the corresponding entry v1= DF of Factor A = 2, and V2 = Residual = 8. From the table we get the value of 4.459
So the 4.459 is the critical value, the crossing point between the H0: (Null Hypothesis) and H1.
And you know compare it to the value from the ANOVA table which is 6.43.
Since 6.43 is greater than 4.459, this means that:
We reject the H0(null) and conclude that there is a difference in the average number of people throughout the day.
If they asked you to test FActor B at 5% as well, you would check the F-Distribution table at 5%, 4, 8 and would find the value 3.838
So here we would not reject the Null Hypothesis because the F-Value from the ANOVA table is 3.57 which is less than the Critical Value found from the Distribution table.