How to find the Utility Maximization Bundle?
In Economics, we study all sorts of situations. Here we want to optimize the best possible combination of goods and services a consumer acquires.
Let’s say we want to find out the best possible bundle that Sarah can get.
x = Beer that costs $4
y = Chips that cost $5
I = Sarah’s Income = $120
We now need a utility function. Let’s say it is u(x,y) = 3xy^2
Since we are combining two goods, and we have an Income variable and prices for both x and y variables, we are essentially presented with a problem to find the quantities of x and y respectively.
So our Budget line comes in the form of the following equation:
Budget line = I = Price of X * X + Price of Y * Y
Since we are on a budget constraint, this is called the budget line. It is the combination that you can get on a specific budget of both goods. Like you have a $10 budget, apples cost $1, beers cost $3, so all the possible combinations between both will be represented on that line.
The line is downward sloping because when you get all your budget used on one item you spend 0 on the other.
This Budget line is represented by the following equation:
Y = – (Px/Py)*X + b or in another form:
Income = Price of X * Quantity of X + Price of Y * Quantity of Y
In our example:
$120 = $4x + $5y
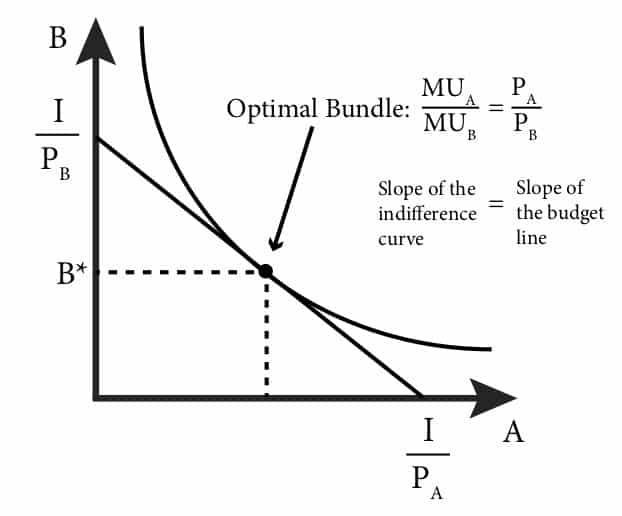
So, our budget line represents our budget constraint. What about that other concave line on top?
This line represents the indifference curve. It means that any point on that line gives us the same level of satisfaction. Same as when we were talking about points on the Production Possibilities curve, here if we had an indifference curve inside the triangle formed by the budget contraint line it would not be optimal, on the other hand, an indifference curve outside our budget constraint would be unattainable on this specific budget.
So this leads us to a point where we need to find the intersectio where both these lines meet. Also called the Optimal Bundle.
This point is given by the coordinates x and y where the Marginal Utility of X divided by the Marginal Utility of Y is equal to the Price of X divided by the Price of Y: MUx/MUy = Px/Py
To solve this, we start with our function u(x,y) = 3xy^2 and find the derivative in respect to x and the derivative in respect to y. This will give us the slope of the line. This is also called the MRS of Marginal Rate of Substitution where:
MRS = – MUx / MUy = (MUx)’ / (MUy)’
Note: you can drop the negative sign since you are equalling two expressions:
-MUx/MUy = -Px/Py which is equivalent to MUx/MUy = Px/Py
Remember: Marginal Rate of Substitution (MRS) is the slope of the Utility Line(Indifference Curve).
MUx = dU/dX = 3y^2
MUy =dU/dy = 6xy
So MUx/MUy = 3y^2 / 6xy = y/2x
Since we are equalling both expressions:
MUx/MUy = Px/Py so
y/2x = 4/5
Doing some simplification we get: y = 8/5 * x
We can now go back to the Budget line and substitute this found y expression so we get:
120 = 4x + 5(8/5*x)
Simplifying we get x = 10
To get y we do the same thing:
120 = 4(10) + 5y
which get us y = 16
So Sarah’s Utility is maximized when she buys 10 beers and 16 bags of chips.
To get the total utils you plug these numbers in the utility function:
u(x,y) = 3xy^2
Substituting the numbers we get:
u(10,16) = 3(10)(16)^2 = 7,680 utils


